1. රූපයෙහි පෙන්වා ඇති පරිදි $P, Q$ හා $R$ දුම්රිය ස්ථාන තුනක් $PQ = \pu{140 km}$ හා $QR = \pu{a km}$ වන පරිදි සරල රේඛාවක පිහිටා ඇත. කාලය $t = 0$ දී $A$ දුම්රියක් $P$ හි දී නිශ්චලතාවයෙන් ආරම්භ කර $Q$ දෙසට $f \pu{kmh-2}$ නියත ත්වරණයෙන් පැය භාගයක් ගමන් කර කාලය $t = \frac{1}{2}h$ හි දී එයට තිබූ ප්‍රවේගය පැය තුනක කාලයක් පවත්වාගෙන යයි. ඉන්පසු එය $f \pu{kmh-2}$ නියත මන්දනයෙන් ගමන් කර $Q$ හි දී නිශ්චලතාවට පැමිණෙයි. කාලය $t = 1h$ හි දී තවත් $B$ දුම්රියක් $R$ හි දී නිශ්චලතාවයෙන් ආරම්භ කර $Q$ දෙසට පැය $T$ කාලයක් $2f \pu{kmh-2}$ නියත ත්වරණයෙන් ද ඉන්පසු $f \pu{kmh-2}$ නියත මන්දනයෙන් ද ගමන් කර $Q$ හි දී නිශ්චලතාවට පැමිණෙයි. දුම්රිය දෙක ම එක ම මෙහොතේ දී නිශ්චලතාවට පැමිණේ. එක ම රූපසටහනක $A$ හා $B$ හි චලිත සඳහා ප්‍රවේග-කාල ප්‍රස්තාරවල දළ සටහන් අඳින්න.

ඒ නයින් හෝ අන් අයුරකින් හෝ, $f = 80$ බව පෙන්වා, $T$ හි හා $a$ හි අගයන් සොයන්න.

2. නැවක් පොළොවට සාපේක්ෂව $u$ ඒකාකාර වේගයෙන් බටහිර දෙසට යාත්‍රා කරන අතර බෝට්ටුවක් පොළොවට සාපේක්ෂව $\frac{u}{2}$ ක ඒකාකාර වේගයෙන් සරල රේඛීය පෙතක යාත්‍රා කරයි. එක්තරා මොහොතක දී, බෝට්ටුවෙන් $d$ දුරකින් උතුරෙන් නැගෙනහිරට $\frac{\pi}{3}$ ක කෝණයකින් නැව පිහිටයි.
   1. බෝට්ටුව පොළොවට සාපේක්ෂව උතුරෙන් බටහිරට $\frac{\pi}{6}$ ක කෝණයක් සාදන දිශාවට යාත්‍රා කරයි නම් බෝට්ටුවට නැව අල්ලාගත හැකි බව පෙන්වා, එයට නැව අල්ලා ගැනීමට ගතවන කාලය $\frac{2d}{\sqrt{3}u}$ බව පෙන්වන්න.
   2. බෝට්ටුව පොළොවට සාපේක්ෂව උතුරෙන් නැගෙනහිරට $\frac{\pi}{6}$ ක කෝණයක් සාදන දිශාවට යාත්‍රා කරයි නම් නැවට සාපේක්ෂව බෝට්ටුවේ වේගය $\frac{\sqrt{7}u}{2}$ බව පෙන්වා, නැව සහ බෝට්ටුව අතර කෙටිම දුර $\frac{d}{2\sqrt{7}}$ බව පෙන්වන්න.

1. රූපයෙහි $ABC$ ත්‍රිකෝණය, $A\hat{C}B = \alpha, A\hat{B}C = \frac{\pi}{2}$ හා $AB = 2a$ වූ $BC$ 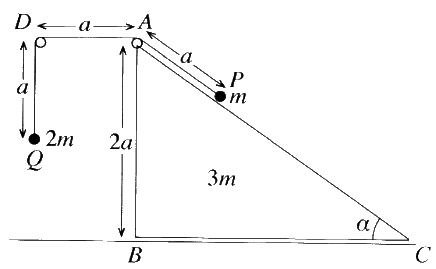අඩංගු මුහුණත සුමට තිරස් ගෙබිමක් මත තබන ලද ස්කන්ධය $3m$ වන සුමට ඒකාකාර කුඤ්ඤයක ගුරුත්ව කේන්ද්‍රය තුළින් වූ සිරස් හරස්කඩ වේ. $AC$ රේඛාව, එය අඩංගු මුහුණතෙහි උපරිම බෑවුම් රේඛාවක් වේ. $D$ ලක්ෂ්‍යය, $AD$ තිරස් වන පරිදි $ABC$ තලයෙහි වූ අචල ලක්ෂ්‍යයකි. $A$ හා $D$ හි සවිකර ඇති සුමට කුඩා කප්පි දෙකක් මතින් යන දිග $3a$ වූ සැහැල්ලු අවිතත්‍ය තන්තුවක දෙකෙළවරට පිළිවෙළින් ස්කන්ධය $m$ හා $2m$ වූ $P$ හා $Q$ අංශු දෙක ඈඳා ඇත. රූපයේ දැක්වෙන පරිදි $P$ අංශුව $AC$ මත අල්වා තබා $AP = AD = DQ = a$ වන පරිදි $Q$ අංශුව නිදහසේ එල්ලෙමින් පද්ධතිය නිශ්චලතාවයෙන් මුදා හරිනු ලැබේ. $Q$ අංශුව ගෙබිමට ළඟා වීමට ගන්නා කාලය නිර්ණය කිරීමට ප්‍රමාණවත් සමීකරණ ලබා ගන්න.

 

 

 

 

2. රූපයේ දැක්වෙන පරිදි $ABCDE$ සුමට තුනී කම්බියක් සිරස් තලයක සවි කර ඇත. $ABC$ කොටස $O$ කේන්ද්‍රය හා අරය $a$ වූ අර්ධ වෘත්තයක් වන අතර $CDE$ කොටස කේන්ද්‍රය $A$ හා අරය $2a$ වූ වෘත්තයක් හතරෙන් කොටසකි. $A$ හා $C$ ලක්ෂ්‍ය $O$ හරහා යන සිරස් රේඛාවේ පිහිටන අතර, $AE$ රේඛාව තිරස් වේ. ස්කන්ධය $m$ වූ කුඩා සුමට $P$ පබළුවක් $A$ හි තබා තිරස්ව $\sqrt{\frac{ga}{2}}$ ප්‍රවේගයක් දෙනු ලබන අතර එය කම්බිය දිගේ චලිතය ආරම්භ කරයි.

$\overrightarrow{OA}$ සමග $\theta (0 \le \theta \le \pi)$ කෝණයක් $\overrightarrow{OP}$ සාදන විට $P$ පබළුවේ $v$ වේගය, $v^2 = \frac{ga}{2}(5 - 4\cos \theta)$ මගින් දෙනු ලබන බව පෙන්වන්න.
ඉහත පිහිටීමේ දී කම්බිය මගින් $P$ පබළුව මත ඇති කරන ප්‍රතික්‍රියාව සොයා, $P$ පබළුව $\theta = cos^{-1} (\frac{5}{6})$ වූ ලක්ෂ්‍යය පසු කරන විට එය එහි දිශාව වෙනස් කරන බව පෙන්වන්න.
$P$ පබළුව $E$ හි දී කම්බියෙන් ඉවත් වීමට මොහොතකට පෙර එහි ප්‍රවේගය ලියා දක්වා එම මොහොතේ දී කම්බිය මගින් $P$ පබළුව මත ඇති කරන ප්‍රතික්‍රියාව සොයන්න.

රූපයේ දැක්වෙන පරිදි $AB = 2a, BC = a$, $CD = 2a$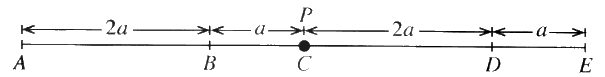 හා $DE = a$ වන පරිදි සුමට තිරස් මේයක් මත $A, B, C, D$ හා $E$ ලක්ෂ්‍ය එම පිළිවෙළින් සරල රේඛාවක් මත පිහිටා ඇත. ස්වභාවික දිග $2a$ හා ප්‍රත්‍යස්ථතා මාපාංකය $kmg$ වන සැහැල්ලු ප්‍රත්‍යස්ථ තන්තුවක එක් කෙළවරක් $A$ ලක්ෂ්‍යයට ඇඳා ඇති අතර අනෙක් කෙළවර ස්කන්ධය $m$ වන $P$ අංශුවකට ඈඳා ඇත. ස්වභාවික දිග $a$ හා ප්‍රත්‍යාස්ථතා මාපාංකය $mg$ වන තවත් සැහැල්ලු ප්‍රත්‍යස්ථ තන්තුවක එක් කෙළවරක් $E$ ලක්ෂ්‍යයට ඇඳා ඇති අතර අනෙක් කෙළවර $P$ අංශුවට ඈඳා ඇත.
$P$ අංශුව $C$ හි අල්වා තබා මුදා හල විට, එය සමතුලිතතාවේ පවතී. $k$ හි අගය සොයන්න.
දැන්, $P$ අංශුව $D$ ලක්ෂ්‍යයට ළඟා වන තෙක් $AP$ තන්තුව ඇද නිශ්චලතාවයේ සිට මුදා හරිනු ලැබේ. $D$ සිට $B$ දක්වා $P$ හි චලිත සමීකරණය $\ddot{x} + \frac{3g}{a}x = 0$ මගින් දෙනු ලබන බව පෙන්වන; මෙහි $CP = x$ වේ. $\dot{x}^2 = \frac{3g}{a}(c^2 – x^2)$ සූත්‍රය භාවිතයෙන් $P$ අංශුව $B$ ට ළඟා වන විට එහි ප්‍රවේගය $3\sqrt{ga}$ බව පෙන්වන්න; මෙහි $c$ යනු විස්තරය වේ.
$P$ අංශුව $B$ වෙත ළඟා වන විට එයට ආවේගයක් දෙනු ලබන්නේ ආවේගයෙන් මොහොතකට පසු $P$ හි ප්‍රවේගය $\overrightarrow{BA}$ දිශාවට $\sqrt{ag}$ වන පරිදි ය.
$B$ පසු කිරීමෙන් පසු ක්ෂණික නිසලතාවට පත්වන තෙක් $P$ හි චලිත සමීකරණය $\ddot{y} + \frac{g}{a}y = 0$ මගින් දෙනු ලබන බව පෙන්වන්න; මෙහි $DP = y$ වේ. $D$ වලින් පටන් ගත් $P$ අංශුව දෙවන වතාවට $B$ වෙත පැමිණීමට ගන්නා මුළු කාලය $2\sqrt{\frac{a}{g}} \left( \frac{\pi}{3\sqrt{3}} + \cos^{-1} \left( \frac{3}{\sqrt{10}} \right) \right)$ බව පෙන්වන්න.

1. $\mathbf{a}$ හා $\mathbf{b}$ යනු ඒකක දෙශික දෙකක් යැයි ගනිමු.

$O$ මූලයක් අනුබද්ධයෙන් $A, B$ හා $C$ ලක්ෂ්‍ය තුනක පිහිටුම් දෙයික පිළිවෙළින් $12\mathbf{a}$, $18\mathbf{b}$ හා $10\mathbf{a} + 3\mathbf{b}$ වේ.
$\mathbf{a}$ හා $\mathbf{b}$ ඇසුරෙන් $\overrightarrow{AC}$ හා $\overrightarrow{CB}$ ප්‍රකාශ කරන්න. $A, B$ හා $C$ ඒක රේඛීය බව අපෝහනය කර, $AC : CB$ සොයන්න. $OC = \sqrt{139}$ බව දී ඇත. $A\hat{O}B = \frac{\pi}{3}$ බව පෙන්වන්න.

2. $ABCD$ යනු $AB = 2m$ හා $B\hat{A}D = \frac{\pi}{3}$ වූ රොම්බසයකි. 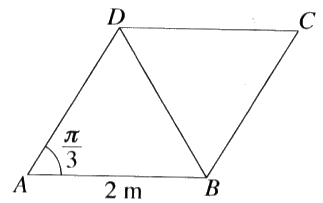විශාලත්වය $\pu{10N}$, $\pu{2N, 6N, PN}$ හා $\pu{Q N}$ වූ බල පිළිවෙළින් $AD, BA, BD, DC$ හා $CB$ දිගේ අක්ෂර අනුපිළිවෙළින් දැක්වෙන දිශාවලට ක්‍රියා කරයි. සම්ප්‍රයුක්ත බලයේ විශාලත්වය $\pu{10 N}$ ද එහි දිශාව $BC$ ට සමාන්තර $B$ සිට $C$ අතට වූ දිශාව බව ද දී ඇත. $P$ හා $Q$ හි අගයන් සොයන්න.

සම්ප්‍රයුක්ත බලයෙහි ක්‍රියා රේඛාව, දික් කරන ලද $BA$ හමුවන ලක්ෂයට $A$ සිට ඇති දුර ද සොයන්න.
දැන්, සම්ප්‍රයුක්ත බලය $A$ හා $C$ ලක්ෂ්‍ය හරහා යන පරිදි වාමාවර්ත අතට ක්‍රියා කරන සූර්ණය $\pu{M Nm}$ වූ යුමයක් ද $CB$ හා $DC$ දිගේ අක්ෂර අනුපිළිවෙළින් දැක්වෙන දිශාවලට ක්‍රියා කරන එක එකෙහි විශාලත්වය $\pu{F N}$ වූ බල දෙකක් ද පද්ධතියට එකතු කරනු ලැබේ. $F$ හා $M$ හි අගයන් සොයන්න.

1. එක එකෙහි දිග $2a$ වන $AB, BC$ හා $CD$ 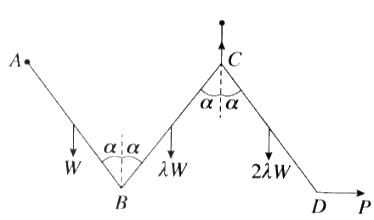ඒකාකාර දඬු තුනක් $B$ හා $C$ අන්තවල දී සුමට ලෙස සන්ධි කර ඇත. $AB, BC$ හා $CD$ දඬුවල බර පිළිවෙළින් $W, \lambda W$ හා $2\lambda W$ වේ. $A$ කෙළවර අචල ලක්ෂ්‍යයකට සුමට ලෙස අසව් කර ඇත. රූපයේ දැක්වෙන පරිදි දඬු සිරස් තලයක සමතුලිතව තබා ඇත්තේ $A$ හා $C$ එකම තිරස් මට්ටමේ ද දඬු එක එකක් සිරස සමග $\alpha$ කෝණයක් සාදන පරිදි ද $C$ සන්ධියට හා $C$ සන්ධියට සිරස්ව ඉහළින් වූ අචල ලක්ෂයකට ඇඳු සැහැල්ලු අවිතථ්‍ය තන්තුවක් මගින් හා $D$ අන්තයට යෙදූ තිරස් $P$ බලයක් මගිනි. $\lambda = \frac{1}{3}$ බව පෙන්වන්න.

$B$ හි දී $CB$ මගින් $AB$ මත ඇති කරන බලයේ තිරස් හා සිරස් සංරචක පිළිවෙළින් $\frac{W}{3} \tan \alpha$ හා $\frac{W}{6}$ බව ද පෙන්වන්න.

 

 

 

2. යාබද රූපයේ දැක්වෙන රාමු සැකිල්ල සාදා ඇත්තේ $A, B, C$ හා $D$ හි දී නිදහසේ සන්ධි කරන ලද එක එකෙහි දිග $2a$ වන $AB$, $BC,CD,DA$ හා $BD$ සැහැල්ලු දඬු මගිනි. $B$ හා $D$ හි දී පිළිවෙළින් $W$ හා $2W$ වන භාර ඇත. රාමු සැකිල්ල $A$ හි දී සුමටව අචල ලක්ෂ්‍යයකට අසව් කර $AB$ තිරස්ව ඇතිව සමතුලිතතාවේ තබා ඇත්තේ $C$ හි දී සිරස්ව ඉහළට යොදන ලද $P$ බලයක් මගිනි. $W$ ඇසුරෙන් $P$ හි අගය සොයන්න.

බෝ අංකනය භාවිතයෙන්, ප්‍රත්‍යබල සටහනක් ඇඳ ඒ නයින්, දඬුවල ප්‍රත්‍යාබල ආතති ද තෙරපුම් ද යන්න සඳහන් කරමින් ඒවා සොයන්න.

1. පතුලේ අරය $r$ ද හා උස $h$ වූ ඒකාකාර ඝන ඍජු වෘත්තාකාර කේතුවක ස්කන්ධ කේන්ද්‍රය පතුලේ කේන්ද්‍රයේ සිට $\frac{h}{4}$ දුරකින් ද
2. අරය $r$ ද වන ඒකාකාර ඝන අර්ධගෝලයක ස්කන්ධ කේන්ද්‍රය, කේන්ද්‍රයේ සිට $\frac{3r}{8}$ දුරකින් ද පිහිටන බව පෙන්වන්න.

පතුලේ අරය $2a$ හා උස $4a$ ඒකාකාර ඝන ඍජු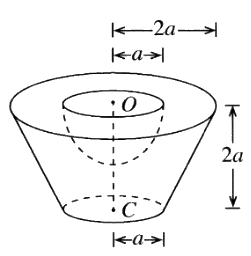 වෘත්ත කේතුවක ජින්නකයකින් ඝන අර්ධ ගෝලයක් ඉවත් කර සාදා ඇති $S$ වංගෙඩියක් යාබද රූපයේ දැක්වේ. ජින්නකයේ ඉහළ වෘත්තාකාර මුහුණත අරය හා කේන්ද්‍රය පිළිවෙළින් $2a$ හා $O$ වන අතර පහළ වෘත්තාකාර මුහුණත සඳහා ඒවා පිළිවෙළින් $a$ හා $C$ වේ. ජින්නකයේ උස $2a$ වේ. ඉවත් කළ ඝන අර්ධ ගෝලයෙහි අරය හා කේන්ද්‍රය පිළිවෙළින් $a$ හා $O$ වේ.
$S$ වංගෙඩියේ ස්කන්ධ කේන්ද්‍රය $O$ සිට $\frac{41}{48}a$ දුරකින් පිහිටන බව පෙන්වන්න.

 

$S$ වංගෙඩිය, එහි පහළ වෘත්තාකාර මුහුණත, 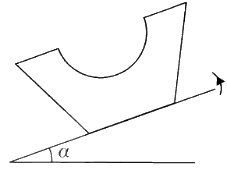තලය ස්පර්ශ කරමින් රළු තිරස් තලයක් මත තබා ඇත. දැන්, තලය සෙමෙන් උඩු අතට ඇල කරනු ලැබේ. වංගෙඩිය හා තලය අතර ඝර්ෂණ සංගුණකය $0.9$ වේ. $\alpha < \tan^{-1}(0.9)$ නම්, වංගෙඩිය සමතුලිතතාවේ පවතින බව පෙන්වන්න; මෙහි $\alpha$ යනු තලයේ තිරසට ආනතිය වේ.

1. එක්තරා කර්මාන්තශාලාවක අයිතමවලින් $50\%$ ක් $A$ යන්ත්‍රය නිපදවන අතර ඉතිරිය $B$ හා $C$ යන්ත්‍ර මගින් නිපදවනු ලැබේ. $A, B$ හා $C$ යන්ත්‍ර මගින් නිපදවනු ලබන අයිතමවලින් පිළිවෙළින් $1\%, 3\%$ හා $2\%$ ක් දෝෂ සහිත බව දනිමු. සසම්භාවීව තෝරාගත් අයිතමයක් දෝෂ සහිත වීමේ සම්භාවිතාව $0.018$ බව දී ඇත. $B$ හා $C$ යන්ත්‍ර මගින් නිපදවනු ලබන අයිතමවල ප්‍රතිශත සොයන්න.

සසම්භාවී ලෙස තෝරාගත් අයිතමයක් දෝෂ සහිත බව දී ඇති විට, එය $A$ යන්ත්‍රය මගින් නිපදවන ලද එකක් වීමේ සම්භාවිතාව සොයන්න.

2. එක්තරා කර්මාන්තශාලාවක සේවකයින් $100$ දෙනකු තම නිවසේ සිට සේවා ස්ථානයට ගමන් කිරීමට ගනු ලබන කාලය (මිනිත්තුවලින්) පහත වගුවේ දී ඇත:

සේවකයින් ගණන්	ගනු ලබන කාලය
$0-20$	$10$
$20-40$	$30$
$40-60$	$40$
$60-80$	$10$
$80-100$	$10$

ඉහත දී ඇති ව්‍යාප්තියේ මධ්‍යන්‍යය, සම්මත අපගමනය හා මාතය නිමානය කරන්න.
පසුව, $80 - 100$ පන්ති ප්‍රාන්තරයේ සිටි සියලු ම සේවකයින් කර්මාන්තශාලාව ආසන්නයේ පදිංචියට ගොස් ඇත. එයින්, $80 - 100$ පන්ති ප්‍රාන්තරයේ සංඛ්‍යාතය $10$ සිට $0$ දක්වා ද $0-20$ පන්ති ප්‍රාන්තරයේ සංඛ්‍යාතය $10$ සිට $20$ දක්වා ද වෙනස් විය.
නව ව්‍යාප්තියේ මධ්‍යන්‍යය, සම්මත අපගමනය හා මාතය නිමානය කරන්න.